Assignment #6

1. Use bilinear interpolation on the skewed and rotated image from Assignment 5.

bigT=255.0*ones(256);
bigT(30:79,64:191)=zeros(50,128);
bigT(50:199,111:146)=zeros(150,36);
newmatrix=255*ones(256);
for x=1:256; for y=1:256;
u=x*cos(5*pi/6)+y*sin(5*pi/6);
v=-x*sin(5*pi/6)+y*cos(5*pi/6);
a=u;
b=mod((v-2*u),256)+1;
r=floor(a);
s=floor(b);
if ((r>0) & (r<256)>0) & (s<256));
newmatrix(x,y)=[1-a+r, a-r]*[bigT(r,s),bigT(r,s+1); bigT(r+1,s),bigT(r+1,s+1)]*[1-b+s;b-s];
end; end; end; imshow(newmatrix)


2. Create a 256 x 256 matrix with 1's in the i,i+1 positions.

A=tril(ones(256),1);
B=tril(ones(256),0);
A-B


3. Determine the average colour:

a) F(:,:,1)=ones(100);
F(:,:,2)=tril(ones(100));
F(:,:,3)=zeros(100);

size(F)
ans=
100 100 3

aveF=sum(sum(M))/100/100
aveF=
ans(:,:,1)=1
ans(:,:,2)=0.50500
ans(:,:,3)=0

A(:,:,1)=1;
A(:,:,2)=0.505;
A(:,:,3)=0;



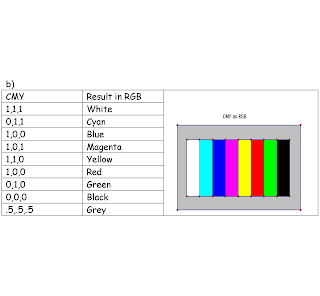
b) Using the rainbow picture from Assignment 4:

A=zeros(256);
B=ones(256);
C=[ones(256,1)*[255:-1:0]/255];
D=[ones(256,1)*[0:1:255]/255];

R(:,:,1)=B;
R(:,:,2)=D;
R(:,:,3)=A;

Y(:,:,1)=C;
Y(:,:,2)=B;
Y(:,:,3)=A;

G(:,:,1)=A;
G(:,:,2)=B;
G(:,:,3)=D;

Cy(:,:,1)=A;
Cy(:,:,2)=C;
Cy(:,:,3)=B;

Bl(:,:,1)=D;
Bl(:,:,2)=A;
Bl(:,:,3)=B;

Ma(:,:,1)=B;
Ma(:,:,2)=A;
Ma(:,:,3)=C;

RB=[R,Y,G,Cy,Bl,Ma];

size(RB)
ans:
256 1536 3
aveRB=sum(sum(RB))/256/1536
aveRB=
ans(:,:,1)=0.50000
ans(:,:,2)=0.50000
ans(:,:,3)=0.50000




b) I am still trying to get images into Octave...

Assignment #5

1. Here are the commands that create a white circle in a black square:

A=zeros(256);
for x=1:256;
for y=1:256;
if (x-128)^2 + (y-128)^2 <=2500;

A(x,y)=1;

endif;

endfor;

imshow(A*255)

2. To get the three circles, in colour:

A=zeros(256);

B=zeros(256);

C=zeros(256);

for x=1:256;

for y=1:256;

if (x-93)^2 + (y-128)^2<=2500;

A(x,y)=1;

endif;

if (x-153)^2 + (y-93)^2<=2500;

B(x,y)=1;

endif;

if (x-153)^2 + (y-153)^2 <=2500;

C(x,y)=1;

endif;

endfor;

endfor;

E(:,:,1)=A*255;

E(:,:,2)=B*255;

E(:,:,3)=C*255;

imshow(E)


3. bigT=255.0*ones(256);
bigT(30:79,64:191)=zeros(50,128);
bigT(50:199,111:146)=zeros(150,36);
imshow(bigT)


bigT1=255*ones(256);
function retval=newy(x,y,s)
retval=y+mod(x*s,256)+1;
endfunction

for x=1:256;
f or y=1:256;
y1=int32(newy(x,y,2));

if(y1>256)
y1=y1-256;
end;

bigT1(x,y1)=bigT(x,y);
endfor;
endfor;




bigT2=ones(256);
for x=1:256;
for y=1:256;

newx=int32(mod(x*cos(5*pi/6)-y*sin(5*pi/6),256)+1);
newy=int32(mod(x*sin(5*pi/6)+y*cos(5*pi/6),256)+1);

bigT2(newx,newy)=bigT1(x,y);

end;
end;










There's still something not quite right, but it's late and I keep making the same mistakes...like Arnold, I'll be back.


Another look at #3. I have deleted 3.0.0 and am using 3.0.1 again. After trying out several versions of the code posted by classmates, I have a somewhat different set of images. Here goes:

The original BigT:

bigT=255*ones(256);
bigT(30:79,64:191)=zeros(50,128);
bigT(50:199,111:146)=zeros(150,36);

The resized (*2) bigT1

for x=1:256;
for y=1:256;
y1=mod(2*x+y,256)+1;
bigT1(x,y)=bigT(x,y1);
end;
end;




The rotated bigT:

f or x=1:256;
for y=1:256;
x2=x*cos(5*pi/6)-y*sin(5*pi/6);
y2=x*sin(5*pi/6)+y*cos(5*pi/6);
x3=round(x2);
y3=round(y2);
bigT2(mod(x3,256)+1,mod(y3,256)+1)=bigT(x,y);
end;
end;


The resized and rotated bigT:

bigT=255*ones(256);
bigT(30:79,64:191)=zeros(50,128);
bigT(50:199,111:146)=zeros(150,36);
for x=1:256;
for y=1:256;
y1=mod(2*x+y,256)+1;
bigT1(x,y)=bigT(x,y1);
end;
end;

for x=1:256;
for y=1:256;
x2=x*cos(5*pi/6)-y*sin(5*pi/6);
y2=x*sin(5*pi/6)+y*cos(5*pi/6);
x3=round(x2);
y3=round(y2);
bigT2(mod(x3,256)+1,mod(y3,256)+1)=bigT1(x,y);
end;
end;

Assignment #3, Questions 2-6a)

Assignment #4

Octave commands to create:

1. a matrix of 256 x 1 ones: ones(1,256)

2. a matrix of the integers 0 through 255 in a single row: [0:1:255]

3. A column of intergers 0 through 255: [0:1:255]'

4. a 256 x 256 matrix with the rows, all the same, equal to 0 through 255:
ones(256,1)*[0:1:255]

5. a 256 x 256 matrix with the columns, all the same, equal to 0 through 255:
[0:1:255]'*ones(1,256)

6. a 256 x 256 matrix of all zeros: zeros(256)

7. a 256 x 256 matrix all ones: ones(256)

8. a 256 x 256 matrix of the value 128: 128*ones(1,256)

10. display a greyscale image: A=(ones(256,1)*[0:1:255]; imshow(A/255)




11 - 13 the faces of the RGB colour cube: A=uint8(ones(100,1)*[0:1:99]); B=uint8(ones(100,1)*[0:1:99]'; C=uint8(zeros(100));
(These were needed to use 3.0.1 on a Mac)

11. RB face: RB(:,:,1)=A;RB(:,:,2)=C;RB(:,:,3)=B; imshow (RB)

12. RG face: RG(:,:,1)= A; RG(:,:,2)=B; RG(:,:,3)=C; imshow(RG)

13. BG face: BG(:,:,1)=C;BG(:,:,2)=A;BG(:,:,3)=B; imshow(BG)

A different version, using 3.0.0 on a PC:

11 – 16. To show these faces, I set up four basic statements:

octave-3.0.0:1> A=zeros(256);
octave-3.0.0:2> B=ones(256);
octave-3.0.0:3> C=[ones(256,1)*[0:1:255]/255'];
octave-3.0.0:4> D=[ones(256,1)*[0:1:255]/255];

Then I created each face using these commands for the RGB layers:





19-22

A=[1,2,3;4,5,6;7,8,9];
1 2 3
4 5 6
7 8 9

B=eye(3);
1 0 0
0 1 0
0 0 1

C=circshift(B,1);
0 0 1
1 0 0
0 1 0


19. A*C
2 3 0
5 6 0
8 9 0

20. C*A
7 8 9
1 2 3
4 5 6


21. circshift((A,1);
for i+1:columns(A);
A(i,1)=0;
A

0 2 3
0 5 6
0 8 9

22. circhshift(A,1);
A
for i = 1:columns(A);
A(1,i)=0'
A

0 0 0
1 2 3
4 5 6

Assignment #3-Getting started

Assignment 3 - The most time-consuming part of this is trying to get the images to stay put!!

1. With data from the Chromaticity diagram on page 400 I used Excel to create the tables of values which I then put into Octave.

The values were entered as lists: w = wavelength, x = red, y = green, and z = 1-x-y = blue. For the other two graphs, I used a = x/y and b = z/y


Wavelength vs. y

Wavelength vs x/y

Wavelength vs z/y

















6. a)



b) In Photoshop: (with thanks to my son for his expert advice)

- Open the "channels" toolbox
- click on Red so it's the only one selected (the picture will go greyscale because it's just the red channel)
- select all, copy, click RGB so it's in colour again
- go to the layers palette, make a new layer, paste
- click the eye to hide that layer, click the background layer
- go back to channels and do the same thing for the blue channel
- when you're done that, you should have the original background layer,
and two new layers on top, each one greyscale (and hidden)

all you need to do now is click on Layer 1, select all, copy, click the background layer, then go to channels and click on blue, then paste (so what was in red is now in blue)

then do the same for layer 2, pasted in to the red channel

Then click the RGB channel, go back to the layers palette, and delete the extra grey layers.

A smile for a cloudy day...

Assignment #2

1. For this question, I transposed the original table so I could put the combinations in line with the output. The top two rows are the inputs, the first column is the output number (0 - 15)

X .0 0 1 1
Y .0 1 0 1
0. 0 0 0 0 Y AND NOT Y
1 .0 0 0 1 X AND Y
2 .0 0 1 0 NOT(NOT ((X OR Y) AND (NOT (X AND Y)) OR (NOT X))
3 .0 0 1 1 X
4 .0 1 0 0 Y AND (NOT X)
5 .0 1 0 1 Y
6 .0 1 1 0 ((X OR Y) AND (NOT (X AND Y)) AND (NOT X)
7 .0 1 1 1 X OR Y
8 .1 0 0 0 NOT(X OR Y)
9 .1 0 0 1 NOT ((X OR Y) AND (NOT (X AND Y))
10. 1 0 1 0 NOT Y
11 .1 0 1 1 NOT ((X OR Y) AND (NOT (X AND Y)) OR (NOT Y)
12 .1 1 0 0 NOT X
13 .1 1 0 1 NOT ((X OR Y) AND (NOT (X AND Y))) OR (NOT X)
14 .1 1 1 0 NOT(X AND Y)
15 .1 1 1 1 X AND (NOT X)

2. Correction: According to DeMorgan's Law, all 16 outputs can be descibed using combinations of AND and NOT. (as was demonstrated in class Monday)

3. The binary function #0 is associative since f(x,y) , f(f(x,y)z), f(y,z) and f(x,f(y.z)) all return o,o,o,o.

4. There are nine binary arguments if you start with {0,1,2} as possible inputs. (3*3). Based on the two input - one output scheme in the first question (2 inputs = 2^n arguments and 2^n^2 outputs) it seems logical that there should be 3^n^2 outputs for for trinary inputs; 3^3^2 = 19683.

5. (Just read "Alice's" blog...the link provided the answer to this one.) The binary operations NOT, OR, AND, and IMPL are required to express every possible two argument function on trinary operations.

6.








Left -Pic1 AND Pic2
Centre Pic1 OR Pic2
Right NOT(Pic1 IMPL Pic2)

7. Death by poison P
Change in blood chemistry C
Residue R
Puncture marks M
Needle N

P IFF (C XOR R)
(NOT (C XOR R) AND M
M AND N
P XOR (NOT M)

Orders of Magnitude

1. A GB is 2^30 bytes. 64 kB is 2^14 bytes. Dividing gives an answer of 16 384, so the 1 GB memory of today is 16 384 times bigger than the Commodore 64.

2. 4.7 GB is 4.7 * 2^30. 800 K is 800 * 2^10. Dividing gives 6160.384 so you would need approximately 6161 floppy discs to store 1 DVD worth of data.

3. In 1976, the Apple 1 had a speed of 1 MHz (1 * 2^20) (http://www.old-computers.com/museum/computer.asp?c=67&st=1)
The TRS 80 I got in 1982 had a speed of 4 MHz (4 * 2^20) (http://www.old-computers.com/museum/computer.asp?c=242&st=1)

The MacAir (just out) has a speed of 1.8 GHz (1.8 * 2^30) (http://www.apple.com/ca/macbookair/guidedtour/)
The MacPro runs at 3.2 GHz (3.2 * 2^30)

The MacPro is 3276.8 times faster than the Apple 1 and 819 times faster than the TRS 80.

Copying from the internet is cheating (sometimes)

I'm not so worried about students sharing answers to homework assignments...I expect students to collaborate and help each other learn. Where I really worry is around major "tasks" or projects which are done at home or over a period of several days and, of course, tests/exams. If students are surreptitiously sharing information/answers, then the assignment becomes invalid.

Cell phones are a major source of worry in high schools today. Students are often text messaging, watching TV/movies, surfing the net or who knows what else when they should be attending to the lesson or working on a test. The cameras in the phones create a whole new world of cheating possibilities. As far as I know, this is a problem in every school all across the country. As of yet, I haven't heard of any really effective solution.

Open-ended projects are one way to challenge students to use the resources of the internet to come up with creative solutions. The major drawback is that if the assignment is truly open-ended, there is no "answer key" and no right answer...a teacher's nightmare.

I've seen plagiarism as blatant as copying a book review off Amazon and pasting it, word for word, including grammatical and spelling mistakes into an English assignment. Other students have tried to copy ideas by changing a few words or phrases. The social science teachers have "Turnitin.com" which helps them detect plagiarism...I haven't heard of anything similar for math and science.